Cohort Analysis Done Right

By

Use a p-chart to properly monitor shifts in customer churn

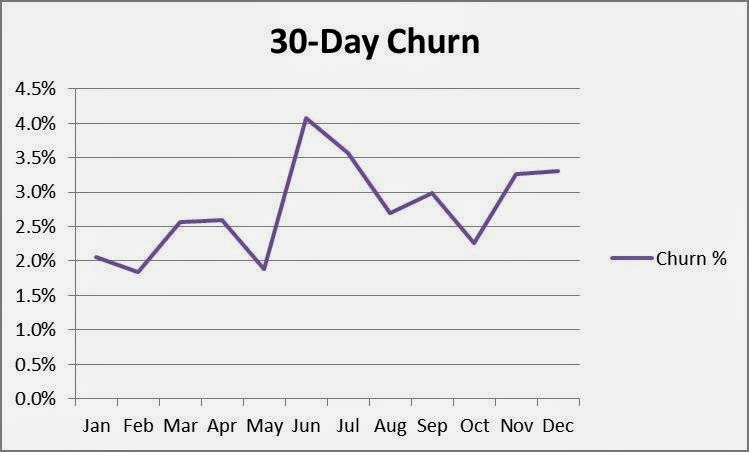
Let’s say you run a Customer Success team and your manager asks you to perform cohort analysis in order to better understand customer churn behaviors. Your customers renew on a monthly basis, and you’re interested in measuring their initial fallout rate. Using data collected over the past year, you count the number of users who canceled their subscriptions after the first 30 days and divide that number by the total number of new users during each month.1  Your Excel spreadsheet table is shown below:

 

You then plot the data:

 

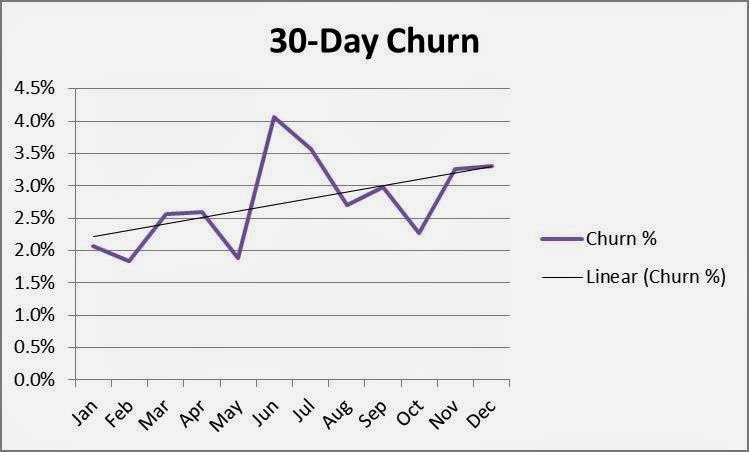
The results concern you. Although the data points vary somewhat, it appears your 30-day churn rate has been increasing all year! Using the trend line function in Excel confirms it—the first month’s churn rate has grown from about 2.2% to 3.2%!!

 

You share this information with your boss and she’s not happy. Clearly your Customer Success team is not doing the job. She expects immediate improvement. Or else. 

Simple, obvious… and wrong

But hold on a minute—you’ve made a serious mistake. You haven’t managed your team poorly. You’ve analyzed your data improperly!

Your error has to do with statistical sampling. Randomness occurs in all data, and experimenters must be careful to separate the “signal” from the “noise.” Statisticians warn of two types of experimental error: 
  • Type 1: False Positive—a result is determined when in fact there’s only randomness 
  • Type 2: False Negative—randomness is determined when in fact there’s a valid result
Without using the proper statistical methods, people can easily jump to the wrong conclusions. Overly simplified, standard tools in Excel make the situation worse. As a result, managers tend to over-react, seeing a problem that isn’t there and making changes that can do more harm than good.2 Managers can also under-react, missing the cues to make changes when it’s time to do so. Most businesspeople lack a strong analytical background, so statistical errors are quite common, often leading to disastrous consequences.   
 

Using the p-chart

Fortunately, manufacturers have been using powerful statistical methods for years, and these practices can easily be applied in software companies. Lean Six Sigma, a quality improvement method, incorporates a broad range of tools that ensure teams properly analyze data and reach valid conclusions. You can use these techniques to your advantage. 

The control chart is a handy Lean Six Sigma tool helping managers avoid Type 1 and Type 2 errors. Control charts are used to determine if a process is in a state of statistical control, i.e., if the observed variation is due to randomness and not any particular cause. There are many different types of control charts depending on the type of data involved, but all follow the same basic structure. The p-chart (or proportion chart) uses the binomial distribution. It is the most appropriate control chart to use in this example because there are only two possibilities (the customer cancels or renews) and results are expressed as percentages.3  

The control charting procedure is as follows:

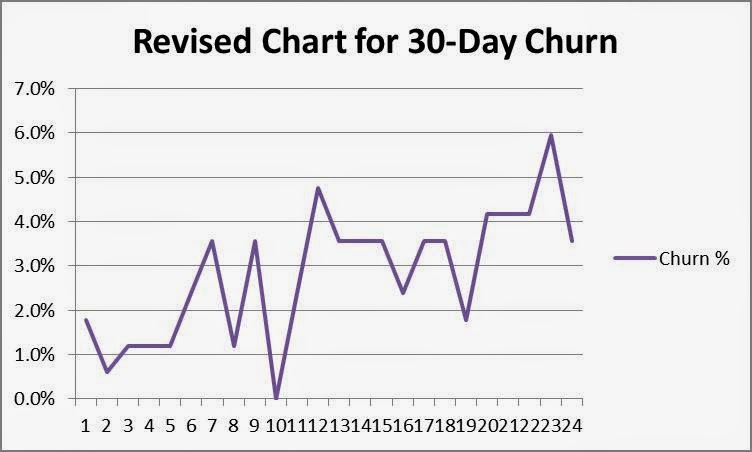
1. Determine rational subgroups. A rational subgroup is a homogeneous set of data that provides a representative sample, such as a batch of parts manufactured during a shift. Many SaaS companies define their subgroups as monthly “cohorts,” the set of new customers who sign up for software during a given month. Usually there’s nothing different about a customer who subscribes in January versus one who subscribes in February, and for the purposes of evaluating churn, it’s more accurate to use sequential, fixed sample sizes instead of varying sample sizes.4  In order to calculate the mean with reasonable accuracy, statisticians recommend using around 25 subgroups. In this case, we’ll choose fixed sample sizes with 168 customers in each of 24 subgroups (4032 customers/24 subgroups = 168 sample customers/subgroup).5  Below is your new sample set:

 

2. Plot the dots. As you can see, the shape looks a little different, but it still appears there’s some trending in the data. 

 

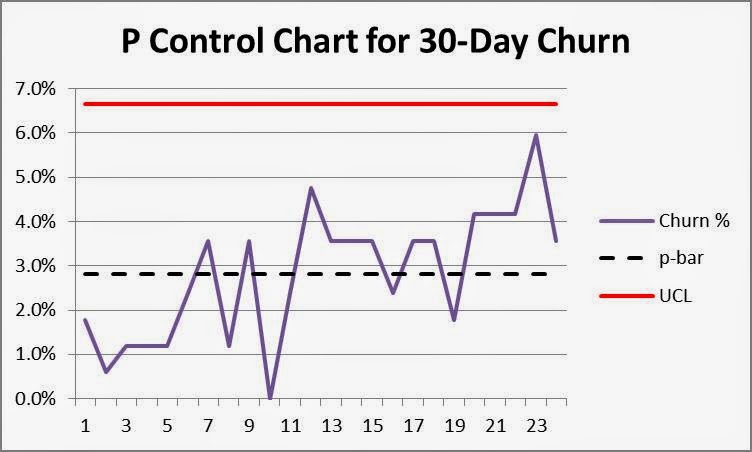
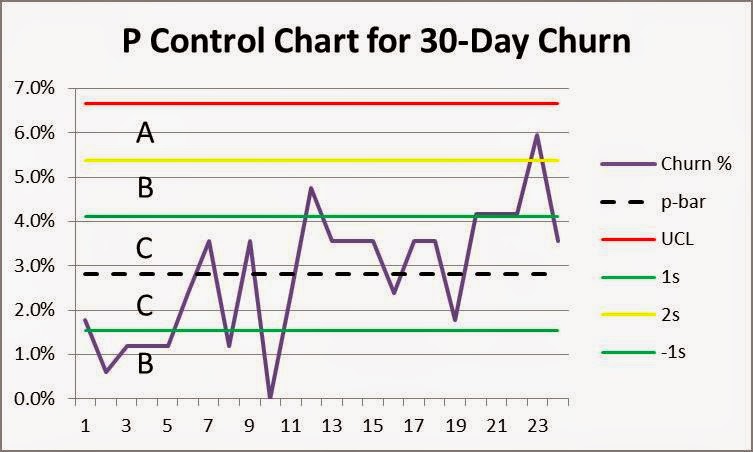
3. Calculate and apply the center line and control limits. 
  • Compute p-bar (or average proportion) for the data set. In this example, 114 out of 4,032 customers churned after the first 30 days, a p-bar of 2.8% (114/4032). Draw this line on the chart. 
  • Calculate the upper process control limit, UCL. This line shows the mean plus three standard deviations. The line is important because the probability of finding a data point more than three standard deviations away from the mean by chance is less than 1%. The UCL calculation for a p-chart is:
UCL = p-bar + 3 * Square Root {p-bar * (1 – p-bar) / n}

where n is the fixed subgroup sample size

In this example, UCL = 0.028 + 3*SQRT {0.028*(1-0.028)/168} = 0.0662 = 6.6%. Add this line to the chart.6  

 

4. Interpret the results. As you can see, most data points fall in the vicinity of p-bar and none exceed the upper process control limit, UCL. This is your first indication that observed variation is likely due to randomness and not any special causes or shifts in your process. For good measure, add lines at +/-1 and +/-2 standard deviations (probabilities of data points in these ranges 68% and 95% respectively) and add them to the chart. Mark zones “C” between the centerline and 1 standard deviation, “B” between 1 and 2 standard deviations, and “A” between 2 and 3 standard deviations from the mean as shown below.

 

Then apply three additional statistical tests to rule out any possibility that something is amiss:7 
  • Nine points in a row in Zone C or beyond on one side of the center line?—NO 
  • Six points in a row steadily increasing or steadily decreasing?—NO 
  • Fourteen points in a row alternating up and down?—NO 
Congratulations, you can breathe a sigh of relief! You’ve correctly established that despite appearances, there’s no trending in the data, contradicting what you originally thought. You explain to your boss that nothing has changed and results are due exclusively to randomness. The data shows that your onboarding process is in a state of statistical control and will routinely produce 30-day churn averaging about 2.8%. What’s more, you can accurately predict that 2/3 of the time future churn will be measured between 1.5% and 4%, 1/3 of the time less than 1.5% or over 5%, and only on rare occasions will it ever exceed 6.6%.  

Next steps 

You can continue to add new data points and monitor process stability using the limits you calculated above and by applying the same interpretation procedure. If any of the four statistical test results are positive, take immediate action and determine the underlying cause. You can use p-control charts to investigate customer defections at other periods of time, such as subscriptions after 60 days, 90 days, or upon annual renewal. Several Lean Six Sigma statistical packages are commercially available online (many of which are SaaS), making control charting much easier. 

Once your Customer Success process is stable, it’s possible to systematically improve it. Although keeping things under control is always your first priority, making things better is your end goal. In my next blog, I’ll describe how Lean Six Sigma methods can be used to help you improve customer retention.

 

Did you enjoy this article? Subscribe to Excel-lens now and never miss another post.

 

Notes:

 

  1. Technically, calculating ratios when denominators vary causes an “average of the average” problem in which comparing percentages between periods introduces significant measurement error. This discussion was deleted for brevity.
  2. Human over-reaction to Type 1 errors is a fascinating subject, one with neurobiological and evolutionary explanations. It’s beyond the scope of this blog, but humans are preconditioned to see patterns and jump to the wrong conclusions, hence the need for robust application of the Scientific Method.
  3. Note that p-control charts can be used with varying sample sizes under certain circumstances (computing average n or using multiple control limits), and that other types of attribute control charts can be used for smaller sample sizes. For simplicity, this discussion was omitted.
  4. Homogeneity extends to type of customer, including the market segment and associated value proposition, as described in my previous guest blog. If churn behaviors vary significantly by customer type, you should stratify your data and chart each segment separately.
  5. A rule of thumb is to choose subgroup sample sizes for attribute data such that np>5; in this case, churn is about 3%; n>5/0.03 or n>167
  6. Note that in this case, the lower process control limit is negative and can be neglected; this is a “single sided” investigation where the minimum churn is 0.0% and we are interested in detecting a shift upward.
  7. Montgomery, D. C. (2005), Introduction to Statistical Quality Control (5 ed.), Hoboken, New Jersey: John Wiley & Sons, ISBN 978-0-471-65631-9, OCLC 56729567